Bercovitz and Di Marzio Formulae
Practical Examples

Computation

{ John  Bercovitz } and others have developed a formula which includes both the parallax and depth of field factors to give a maximum permissible stereoscopic effect.

When you focus the camera it is best to focus between the nearest and furthest object and then stop down until both are in focus. This is using the hyperfocal distance, as marked on your lens barrel, to get an evenly sharp picture.
This sensible focusing manoeuvre is included in the formula, to allow for magnification of stereoscopic parallax resulting from the lens being racked forward from its infinity setting.
The aim is to have the maximum parallax which can be mounted in a stereo pair and yet retain a stereo window in front of the nearest object. 
(If you have greater parallax than the formula allows, the stereo pair can still be seen in stereo but at the expense of incorrect window, unless you can arrange for "double depth" windows, or "eye poking stereo" as discussed in the section on mounting stereo pairs.)

B =  P/(L-N)  ( LN/F - (L+N)/2 )

B = Stereo Base (distance between the camera optical axes)
P = Parallax aimed for, in mm on the film
L = Largest distance from the camera lens
N = Nearest distance from the camera lens
F = Focal length of the lens

(L-N = D = the front to back depth of the subject. With a bit of luck it is also the depth of field of the image, but does not have to be, especially at macro distances where a big depth of field is hard to achieve.)

If the largest distance (L) is at infinity, Bercovitz says the following applies:

B = P (N/F - 1/2)

The formula is not for orthoscopic viewing.
     orthoscopic viewing.

It gives the greatest stereo effect that can be fused by a beginner.
It has nothing to do with aesthetics. Often you do not want the maximum possible stereo depth in your pictures.

Hyper stereo example: Big baseline

This small anaglyph is easily fused.

The parallax deviation at the deepest mountain is only 3mm on a 17 inch monitor set at 1024x768 pixels.

(Cha-cha hyper stereo photographed by John Wattie)

The 2x bigger anaglyph panorama should still be easy for just about everybody.
Deepest stereoscopic linear parallax is only 6mm on a 17 inch computer monitor (336mm horizontal) running at 1024x768 pixels.
With the monitor resolution set on 800 x 600 pixels, infinity parallax is nearer 8mm, still easy for most people.

Note how the size of the computer monitor and the setting of the video card make a big difference. This shows how the maker of computer anaglyphs or stereo pairs has no control over how the audience will see the result. If you have difficulty, sit further away from the computer monitor.

Distances from The Geographic Atlas of New Zealand:

Nearest Distance: 4.1km
Longest Distance: 16.6km
Focal Length: 7mm Sony V3 = 34mm in 35mm equivalent.
(i.e. 7mm actual focal length on the Sony has the same angle of view as 34mm focal length on a 35mm camera, like the digital Canon 5D).
Base: approximately 100meters (paced out)
Linear Parallax: 0.62mm (1/56 of 35mm): a conservative stereo base which will allow considerable enlargement of the anaglyph and still be viewable by neophytes..

.

Close up stereo example

Example:    Flower in a vase, subject depth 100mm (10cm)    P = 1.2mm (35mm film)   L = 600mm (0.6 meter)  N = 500mm  (0.5 meter)  F = 35mm Then stereo base, B = 96mm In macro photography, the depth of field extends symmetrically forwards and back from the focus point. The focus is determined by focusing half way into the depth of the scene. (550mm in this case). This is different from landscape photography where the depth of field is asymmetric, as demonstrated by the hyperfocal distance. The Davis Modification of the Bercovitz formula gives a much smaller answer: L = 2N = 1000mm all other variables are the same as above B = 1.2/(1000 - 500) * [1000*500 / 35 - (1000 + 500) / 2 ] B = 32mm The Di Marzio Formula for macro photography, where m<2n, gives practically the same answer as the Davis modification. However, it is much easier to calculate the Di Marzio formula, than the Davis Modified Bercovitz formula: B = N / 15 B = 500/15 B = 33mm The 1 in 30 rule gives a very small base: B = N/30 B = 500 / 30 B = 16mm This is so small, the author finds the resulting 3D unrewarding for the effort expended. It is the correct answer, if the far distance is included in the picture, which it hardly ever is in close-up photography. However 1 in 30 is the traditional method, which is advocated in many stereo books and internet sites. Left Right 96mm stereo base, as determined from the Bercovitz formula for a 10cm thick object at 500mm distance.   Right Left The stereo base separation in this example, where the distance to the object is about as far as your computer screen, is more than the inter-ocular distance. Intuitively you would think that has to be wrong, but it works! The large camera separation is possible because the front to back depth of leaves in the vase is only 10cm and the camera focal length is shorter than standard (32mm versus 50mm). The result is stereoscopic depth amplification, but it is easily viewable, just as Bercovitz claims. There is some stretch distortion. The rim of the vase is elliptical and not round, stretched in the direction of view. (A round object is good for checking on stretch and squeeze distortion, as I first found out photographing mushrooms.) By moving backwards and forwards you can find the best viewing distance to minimise the stretch distortion (easier on the bigger X stereo image below). Stereo separation should decrease for close-up subjects (hypo-stereoscopy), but not to the degree suggested by the older workers (1/30 rule). As long as there is no distant background, the base can even increase (but at the expense of depth amplification.) There is no keystone effect in this picture.       keystone effect  camera convergence was not used, but extensive cutting for  window was required. The stereo window was adjusted to lie at the rim of the vase, so leaves project out of the computer screen. stereo window This window is "cheating" by making it too easy to fuse the pictures, but I know they are being viewed on a computer. The aim of my exercise was to show stereo amplification in close-up photography does not result in a picture we find "too distorted," a concept that is not intuitive.

The Davis modification and the Di Marzio equation (which incorporates the Davis modification in its derivation) give a gentle answer for the macro stereo base. The Bercovitz formula gives the maximum possible, the other two give a 3D that many stereoscopists say they prefer. Traditional stereoscopists use the 1/30 rule - but that is far to gentle for the author. If you hold an object close by to examine it, especially using magnifying lenses ("hobby glasses"), the stereo effect you get is closer to the unmodified Bercovitz formula, as this example shows.

When people who have not seen much stereo before are shown pairs taken using the Bercovitz formula, they have not complained. Traditional workers (on a card folio circuit), who always complain if they cannot fuse images, or even if they intermittently see double, have also found the stereo acceptable.

In my experiments, people are happy as long as:

1. There is no window violation,
2. The most distant point is not set too far apart for their eyes,
3. Close objects are not separated from distant objects, with nothing linking them at intermediate distances (which causes large monoscopic areas and obvious diplopia).

Only the "stereo academics" are unhappy with deep stereo!

Eric Scanlen, who is often asked to project his 3D orchids at meetings, tells me he has found the same thing. Even when orchid parts reach out and almost touch the audience's noses, they do not complain! That is an advanced version of "stretch distortion," of objects pointing out through the stereo window, but people enjoy it. A happy audience is the name of the game and "reality" seems to have little to do with it!

Bercovitz curves are available in graph form { here }

Davis Modification

The Bercovitz formula requires such a large stereo base for very shallow close-up objects that the resulting stereo magnification can distort and become disturbing. This is avoided in practice by only using the formula when the most distant plane (L) is more than twice as far away as the near plane (N).

Once L is less than 2N, the formula is adjusted by making L = 2N and this stops the stereo base getting absurdly big. LINK

The Davis correction is built-in to the more recent Di Marzio formulae

Different focal lengths example

Bill Percival was photographed in a studio with electronic flash portrait lighting. 135mm lenses were separated by 135mm stereo base. The forest was photographed with 34mm lenses and a 300mm stereo base. In post-processing, the portrait was superimposed on the forest. Because the Berkovitz formula had been applied to determine the stereo base for both foreground and background stereo pairs, the 3D merges seamlessly, despite the 4 times difference in focal lengths. (35mm equivalent focal lengths on Sony V3 cameras)

Go to Page 2 of stereo mathematics

Di Marzio Formulas

These are best presented in Frank Di Marzio's own words.

The Paul S Boyer formula for macro stereo

B = 106.68*W / F*(M+1)

All measurements are in mm, where:
B = the stereo base,
W = width of the diapositive [36 for full-frame, 31 for European, and 23 for Realist],
F = focal length of the lens, and
M = magnification ratio

The advantages of the Boyer formula are: macro lenses have the magnification factor marked on them, or more often the reciprocal of the magnification. e.g. 1:2 means half size.

There is no need to measure the distance to the subject (which could result in breaking a delicate object or frightening an insect away.)

This procedure is best with the two camera directions operated by screw threads, rather like a mechanical stage on a microscope. (For the "Wattie method," which does not use any calculations or measurements, but is pretty close to the Boyer technique, see practical stereo macro-photography).

1. You adjust the magnification to the desired value on the lens.
2. Move the camera back and forwards to focus it.
3. Then move the camera sideways between two exposures, by the distance B.

Example

M = Magnification ratio = 1:1
F  = Focal length of the lens = 105mm macro
W = Width of the image = 35mm

B = 106.68 * 35 / 105 * (1 + 1)

B = 18.7mm

It so happens, 35mm image width in a 35mm camera can only be achieved by toe-in, which requires rotating the camera on the micro-positioning device.

Frank Di Marzio Magnification Equation

When I e-mailed him about the Boyer equation, Frank did some algebra and came up with an even simpler formula (which is derived in his large technical paper).

B = F (1+ 1/M) / 15

for 1:1 reproduction, this simplifies to:

B = F / 7.5

For example: using a 105mm macro lens at 1:1 reproduction.

Magnification = Extension / Focal Length

M = E / F

The 105mm lens is racked out to 105*2mm from the film = 210mm for 1:1 magnification.
This can be done with extension tubes, so that extension = focal length for 1:1 reproduction

(E = F for a magnification of 1. Remember "extension" is how far the lens is racked out from the infinity focus position. Extension is the length of the extension tubes only if the lens focus is set on infinity. Otherwise you have to add on the distance the lens has been screwed out from its infinity position.)

The object distance from the lens (N), is also 105*2 = 210mm

(Easy to remember: when focus is correct and the lens is set up symmetrically between the object and the film, the magnification is 1. Problems arise with asymmetrical lenses, such as telephoto or extreme wide angle lenses, when a pupillary factor has to be included... )

B = N/15 = 210 / 15
B =  14mm (Di Marzio close-up formula)
Notice how the Focal Length of the lens has canceled out and is not in the formula

B = Fc (1+1/M) / 15
B = 105 (1+1/1) / 15
B = 105 *2 / 15
B = 14mm (Di Marzio magnification formula)

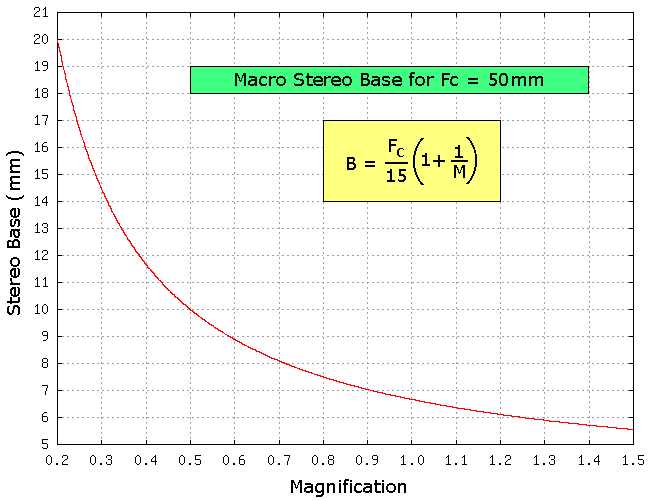
Graph by Frank Di Marzio, June 2005

Magnification also gives the exposure correction needed for extending the lens:

Exposure correction = (M+1)²

Effective f number = (f number marked on the lens)(M+1)

The effective f number is the value to use when calculating the exposure needed from a flash unit. If the magnification is 1:1 and the f number is f8, the effective f number is f16. (Most macro lenses are symmetrical).

Stereo Base for Hyperstereoscopy using Telephoto Lenses

By re-arranging the Bercovitz infinity formula, it is possible to compute how close the nearest object (N) "should be" when changing the stereo base and using a telephoto lens.   stereo base

N = ( BF/P ) + F/2

The graph shown here was prepared by the author for 

35mm format,  where P = 1.2mm: and infinity is in the picture

35mm wide angle lens,   135mm short telephoto   300mm telephoto lens.

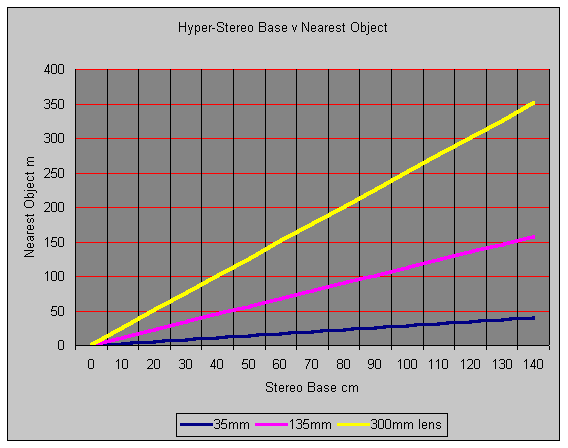
Since these are straight line graphs, the formula for 35mm hyperstereoscopy can be much simplified to:

N = 0.83 F B

B = 1.2N / F
(35mm format)

The observant will realise 1.2mm is the desired parallax in 35mm stereo. (P) You will also realise the "1/30 rule" has been sent to the trash can.

B  = P N /  F

Telephoto hyperstereoscopy with reduced subject depth

As in close-up stereoscopy, the stereo base can be increased if you do NOT include photographic infinity. The size of this correction can be very significant. It is well worth knowing in forest photography, where infinity is obscured by the trees.  This means stereoscopic infinity can be replaced by the deepest plane in the picture.

For example, using the full Bercovitz formula:

• 300mm lens
• N = 100 meters
• L = 150 meters

B (stereo base) = 120cm

If infinity is included in the picture, then B falls to 40cm