08/03/08
|
This paradox in stereoscopic photography is seen with zoom lenses while performing cha-cha, or using two identical cameras on a bar.
The linear parallax between the stereo pictures should be limited below the MAOFD (Maximum acceptable on film deviation).
The linear parallax (P) increases if the:
Nearest distance (N) falls or the
Focal length (F) rises or the
stereo Base (B) rises.
The relationship is expressed in the full Berkovitz formula:
B = P(LN/L-N) (1/F - (L+N)/2LN) ----------(1)
The Nearest allowable distance is familiar to owners of old-fashioned stereo cameras, where the base and the focal length are fixed, and is usually 2 meters.
In ordinary, 2D photography, zooming to telephoto increases the image size.
Stereo photography is more complex because Parallax (P) has to be kept equal or below the MAOFD by using formula (1):
In practical photography with Sony V3 cameras on a fixed base, it seemed to me that the combination of moving back and zooming in, as dictated by the Berkovitz formula, resulted in the image size, at the nearest distance, staying constant.
The image magnification (M) from the simple lens formula is:
M = 1/(N/F - 1)
Substituting for N from the infinity version of the Berkovitz equation into the magnification formula and simplifying resulted in:
M = 1/(B/P - 1/2)
Notice how the Focal length (F) has dropped out.
Magnification depends on the stereo Base and the chosen linear Parallax (MAOFD).
Since in practice the Parallax stays constant, Magnification is determined by the stereo Base.
(Just which consistent Parallax you choose is a personal issue and varies with the viewing technique preferred and how much expertise the audience has at fusing stereoscopic parallax. That is another subject, the mathematics just enables consistency in your decision.)
For a constant linear Parallax (MAOFD) the stereo Base determines the allowable magnification.
No matter how much the lens is zoomed, the Magnification must stay constant.
Constant Magnification is achieved by zooming in and then moving back from the object (increasing N), but keeping the stereo Base (B) unchanged.
I call this paradox "frozen magnification."
This only applies if stereoscopic infinity is in the picture
If the image has reduced depth (portrait photography against a background for example) then the stereo base can rise, despite using increased magnification (such as a telephoto lens). In this case you must use the full Berkovitz equation to find the stereo base, not the simple infinity version.
The PEPAX principle says the stereo base must increase proprtional to the change in focal length to keep the parallax constant. (Double the focal length, double the base). The Berkovitz formula shows this will not work if infinity is in the picture. However, PEPAX will work (within limits) if the subject is shallow.
When using the Berkovitz formula, there is often a problem. The Nearest distance is so far away you cannot measure it (at least not unless you are the proud owner of a laser range-finder, but even those are usually limited to 1 km).
Measure Nearest distance using a wide angle lens (where N is short and more practical to measure).
Notice how big the object is on the digital camera screen.
Do not change the stereo base.
"Frozen magnification" means you can then zoom to telephoto and walk back until the object returns to its original size.
You will be at the correct new Nearest allowable distance for your zoomed lens.
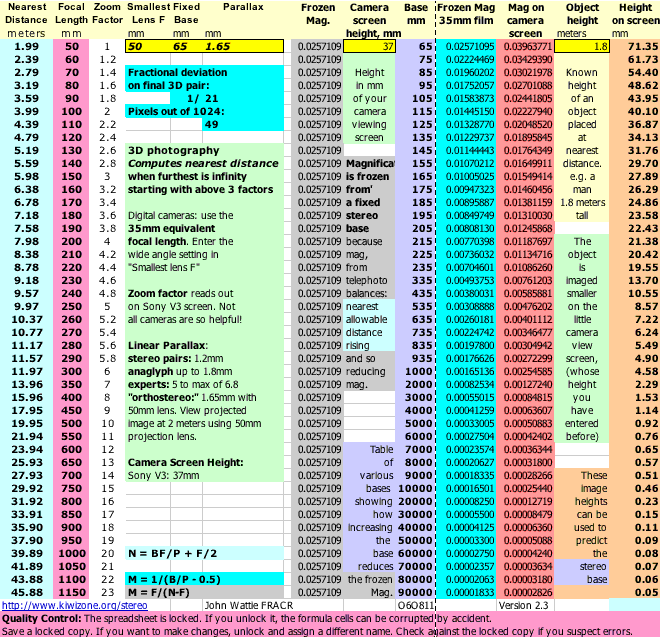
All this is much easier if you read from a spread-sheet on a PDA carried in your pocket.
Spreadsheet Version 2.3 is designed to go with this explanation and includes extra columns to demonstrate how the various formulae merge together. A simpler version is better for use in the field.
After entering the stereo base (B) you plan to use, the height of your digital camera screen, the required Parallax (P) (MAOFD) and the height of a known object which will be at the Nearest allowable distance (N), the Spreadsheet will compute the height in mm that object should be on the camera screen.
All you do then is move forward or back until the object measures the required height on the camera screen.
This works well where people are moving about, just wait until a 180cm man has the predicted height on the camera screen and the person is at N. It also works well for buildings with standard height doors, or standard height buildings, etc.
Perceived stereo depth is determined by the "stereoscopic inverse square law."
Parallax varies as the inverse distance, not the square of the distance.
Using a telephoto lens for stereo will make objects seem flatter: "squeeze," or in extreme examples "card-boarding." The advantage of stereo from a big base is seeing large objects, like mountains, in 3D. A big stereo base has a low "frozen magnification" no matter what the focal length and is not so good for small objects. Mountain 3D is something our human 65mm inter-ocular distance cannot enjoy, without help from hyper-stereo photography, so it is well worth getting the basic geometry correct.
Special conditions apply when L<2N. On paired Sony V3's, where stereo base cannot be reduced below 65mm (base to base), close up magnification is higher with a telephoto setting - but that is another subject!
The Berkovitz formula is a very precise method for determining the stereo base needed to give consistent stereoscopic linear parallax. (MAOFD - maximum on film deviation). Unfortunately it is difficult when photographing in the field to measure the distances required by the formula. In hypersteoscopy, the distance to the nearest object can be several kilometers. Often a map is the best solution.
Mariners measure distance to a lighthouse using a sextant (unless they have radar of course). Knowing the height of a lighthouse above sea-level and then measuring its angular height from the ship allows trigonometry to give the distance.
It is no use carrying a sextant around in your stereo-camera bag. But the camera does allow you to measure image magnification of a known objects. Men for example are around 1.8 meters tall. Measure how tall he is on your camera digital screen and it should be possible to compute how far away he is. Houses and doorways are other examples of known heights.
Computing is not practical in the field unless it is all set up in a spread sheet on your PDA (Personal Digital Assistant). I have prepared a spreadsheet, v2.3, in which you enter:
Berkovitz formula
Once you have the height on screen, look to the left in the table to find the stereo base that is appropriate.
This is not the most logical arrangment for use in the field, but has been set up to show how the formulae were tested.
