There is only one problem with the PePax principle, according to some people writing on the internet, it is wrong!
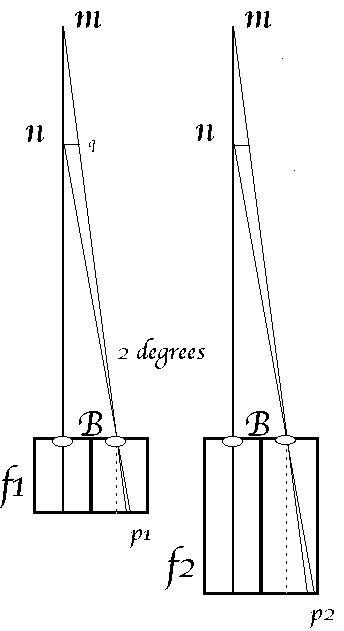
Telephoto lens versus standard lens.
the stereo base, B, is constant
the same two objects, m and n are imaged,
from exactly the same place
only the focal length changes from F1 to F2
The effect on stereo parallax is to change from p1 to p2
By similar triangles:
p2 / p1 = F2 / F1
But this is not the conditions of the PePax principle, where the magnification is fixed. McKay wants to make a distant object the same size and stereo depth as if it were photographed from nearby with a standard stereo camera using short focal length lenses.
Consider a stereo pair taken with everything the same, except the focal length of the lenses (F) is changed.
Let us assume F1 is the standard focal length for the camera format and F2 is a telephoto lens.
MacKay was correct:
The magnification of the image is given by the ratio of focal lengths:
magnification = F2/F1
MacKay was "wrong":
The parallax angle between distant object m and nearer object n is constant (say we set it up as 2 degrees to suit the standard lens).
BUT the linear parallax on the film is magnified, just the same as everything else in the picture is enlarged by F2/F1.
SO the telephoto lens (F2) has a bigger parallax on the image. It has already magnified the stereo depth.
The same thing happens if you enlarge just part of the pictures and mount them as a stereo pair. The parallax is also enlarged. If you have followed the Bercovitz formula to achieve maximum stereo base and then enlarge the prints, you will make the new stereo pair difficult or impossible to mount and fuse.
Doing nothing but change from short focus to telephoto lens gives hyperstereoscopy.
Those who prefer orthostereoscopy will have to reduce the stereo base (B) when shooting telephoto.
But reducing stereo Base as focal length increases is exactly opposite to the PePax principle isn't it?
Yes it is, but the arrangement in the diagram is not PePax. Read on!
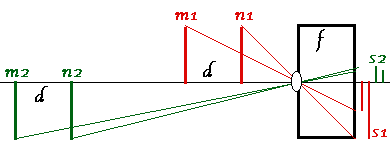
The PePax principle quotes the special case where the magnification is the same despite changing from a standard to a telephoto lens.
Dropping the magnification in telephotography (with a fixed focus lens) can only be done by moving further away from the subject.
To get the same magnification changing from F1 to F2
n must increase in proportion to:
F2 / F1
Now consider the parallax between front and distant objects. If you doodle on the back of an envelope, using similar triangles and the above diagram, the parallax as you get further away from the subject is found to be:
-
Stereo parallax (p) = FBd / mn
-
Simpler than the general Bercovitz formula, because it is for pin-hole cameras, while the general formula includes a depth of field correction for lenses.
The surprising consequence of this parallax equation is:
- magnification of the front object (F/n) decreases linearly with distance but
- parallax between the front and back object decreases by the square of the "average" distance.
(actually the square of the geometric mean distance between front and back object, or by 1 / [m n] ).
So PePax is right: you must do two things to regain "proper" stereo depth when photographing a distant object:
- Increase the magnification (change to a telephoto lens: F is bigger) That also recovers part of the stereo depth which was lost by moving away.
- Increase the stereo base in proportion to F. That recovers the rest of the stereo depth.
Then the stereo parallax is back to "normal".
In other words we must use a quadratic (square) function for the stereo depth but a linear function for the magnification.
Stereo depth perception decreases by the square of the distance: a stereoscopic inverse square law.
Just as McKay said - only he put it differently and confused everybody ever since!
PePax is still not orthostereoscopy, as the attractive purple column to the right explains.
The reason perspective decreases with telephotography comes from the change in magnification with distance.
Magnification on the film changes with focal length in a linear fashion:
by (F / n) for the near object and
by (F/ m) for the distant object.
For a subject with fixed depth, d:
(d = m-n)
the further away you get, m and n get closer to being the same
(m / n approaches 1).
So the difference in magnification between the near object (n) and the distant object (m)
(F / n minus F / m)
drops as we move away.
We say the perspective has decreased in a telephoto picture, because we are losing the size cue of distant objects looking smaller than closer objects.

Variation in stereo base and focal length is shown very nicely by Tony Alderson {here}