version: 06/08/02
version
05.03.08
NEW 05 06 05: Di Marzio equations for stereo base.
08.06.05: Macro stereo base with 50mm lens_ graph
13.06.05: Digital camera depth of field at macro distances.
17.06.05: Di Marzio: depth of field equations at macro distances: pdf file
24.06.05: Di Marzio: diffraction versus f number: pdf file
27/06/05 Di Marzio Formula Derivation in .pdf
4/11/05: Diffraction versus depth of field: practical experiment on a digital camera supplements mathematical theory.
4/12/05: Pixel size versus depth of field (Canon 5D digital camera): experiment gives some unexpected answers!
|
Dr Frank Di Marzio, 46, suffered a fatal heart attack on August 31 2005. A tribute to him has been published by http://www.trinity.unimelb.edu.au/news/media/2005/20050902.shtml The stereoscopic community has lost a great character and I have lost a good friend, who I never met. This web page is now dedicated as a memorial to Frank's clear thinking and skill as a teacher. The numerous E-mails from Frank showing how his contribution to this page developed are now available here. They may clarify some of the complex points he made in the more formal .pdf files. Concepts have continued to develop. Unfortunately, only the .pdf files have Frank's authority now and errors may be creeping in. Feel free to complain in the guest book if you find mistakes. Further details and reviews of Frank's work here |
These are best presented in Frank Di Marzio's own words. He has kindly revised his equations especially for this web site
Simplified version as a .pdf file.
Di Marzio macro stereo formula based on magnification
Di Marzio macro stereo formula, where M is less than 2N here
Di Marzio equations: how they were derived. .pdf file (Large: 1mB)
The remarkable thing is how deceptively simple his equations are.

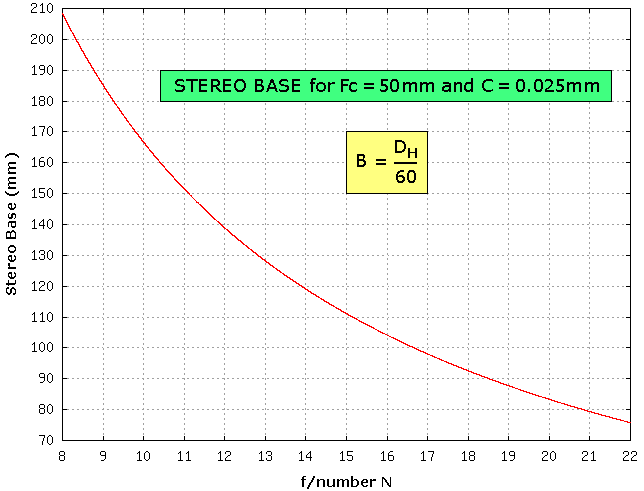
Graph by Frank Di Marzio, June 2005
Stereo base versus the f number which just keeps the near and far points in focus, as read off the hyperfocal scale on the camera lens.
(Or from the automatic depth of field program on some Canon cameras)
Fc = camera lens focal length = 50mm
C = Circle of Confusion = F/2000 = 0.025mm
B = Stereo base
Dh = hyperfocal distance.
This equation is remarkably simple, characteristic of Frank's ability to reduce a formula to its essence.
Close up photography, where the most distant object is less than twice the distance to the furthest object.
B = N/15
B is Stereo Base
N is distance to nearest object
MAOFD = 1.2mm
Note that the focal length of the lens has dropped out of the equation. N/15 applies to any focal length. This is much more subtle than the 1/30 rule, which only applies to standard focal length lenses (and does not apply at all in the macro range).
I successfuly have used this formula in the form:
N = 15B
This was for my Sony V3 pair of cameras mounted horizontally on a bar, where the base cannot be reduced below 135mm (twice the inter-ocular distance). This should be hopeless for close-up photography, but Frank's formula says the lens can be:
N = 15 * 135 = 2025mm from the subject.
Just over 2 meters and the subject looks pretty small, but remember the formula applies to any focal length lens, so you can use a telephoto from 2025mm. This is how I photographed a Tuatara lizard in stereo, an image which has been published twice in magazine articles on stereoscopic photography. The background was closer than twice the distance to the lizard. (The publishers did not ask how it was done, but now you know.) This is not macro photography but it is close-up and with a longer focal length it could become macro.
Note this is a thin lens equation and raises the problem of where on the camera the distance, N, should be measured from. It should be done from the first principle point, but on a big macro lens you have trouble knowing just where that is. On a small digital camera, the lens is short and the distance is easily measured near enough. In this lizard case N could not be measured, but 2 meters was easy to estimate and I could not get closer than that anyway.
When I e-mailed him about the Boyer equation, Frank did some algebra and came up with an even simpler formula (which is derived in his large technical paper).
for 1:1 reproduction, this simplifies to:
For example: using a 105mm macro lens at 1:1 reproduction.
Magnification = Extension / Focal Length
M = E / F
The 105mm lens is racked out to 105*2mm from the film = 210mm for 1:1 magnification.
This can be done with extension tubes, so that extension = focal length for 1:1 reproduction(E = F for a magnification of 1. Remember "extension" is how far the lens is racked out from the infinity focus position. Extension is the length of the extension tubes only if the lens focus is set on infinity. Otherwise you have to add on the distance the lens has been screwed out from its infinity position.)
The object distance from the lens (N), is also 105*2 = 210mm
(Easy to remember: when focus is correct and the lens is set up symmetrically between the object and the film, the magnification is 1. Problems arise with asymmetrical lenses, such as telephoto or extreme wide angle lenses, when a pupillary factor has to be included... )
B = N/15 = 210 / 15
B = 14mm (Di Marzio close-up formula)
Notice how the Focal Length of the lens has canceled out and is not in the formulaB = Fc (1+1/M) / 15
B = 105 (1+1/1) / 15
B = 105 *2 / 15
B = 14mm (Di Marzio magnification formula)
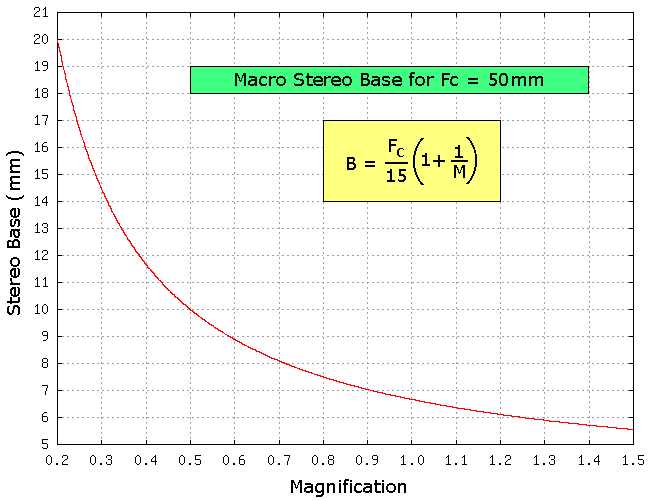
Graph by Frank Di Marzio, June 2005
The effective f number is the value to use when calculating the exposure needed from a flash unit. If the magnification is 1:1 and the f number is f8, the effective f number is f16. (Most macro lenses are symmetrical).