This is Edition 1. Edition 2 has some changes not shown here, but does not cover the whole subject yet.

  Version: 12/03/19

Calculating the stereo base

This has become more critical now twinned (or cha-cha) digital cameras are replacing 35mm film cameras. Just what do you do about zoom lenses and tiny CCD chips?

The secret is to enter 35mm equivalent focal length into the formulae, not the actual focal length, which often you do not know anyway.

• 35mm equivalent focal length is the focal length giving the same horizontal angle of view as on a 35mm film frame with a 2:3 format. Defined this way, "35mm  equivalent" includes both the focal length and the size of the media.
• We then set MAOFD or Maximum Allowable On Film Deviation as computed for a 35mm camera.
• I know, I hear you cry, "film and 35mm are both obsolete now," but digital camera focal lengths are still quoted in 35mm equivalents. This is the only way to get a comparison between different digital formats, and it works in 3D photography too.

For digital cameras: MAOMD = Maximum Allowable On Media Deviation. The media (CCD Chip etc) is hidden inside your tiny digital marvel and you usually have no idea how big it is. MAOMD becomes a big problem. So forget it: use 35mm equivalent measurements. The images from all cameras are enlarged to a consistent size for viewing and so the actual on media measurements do not matter. only the ratio of media size to lens focal length is important. In other words, we are only interested in the camera field of view. (There is always an exception: depth of focus, as we will compute later).

Edition 2: I now use MAD: Maximum Acceptable Deviation

Bercovitz formula

{ John  Bercovitz} and others have developed a formula which includes both the parallax and depth of field factors to give a maximum permissible stereoscopic effect.

1. The Bercovitz full formula is thought to be the best description yet achieved for defining the parameters involved in stereoscopic photography.
2. A simpler Bercovitz formula applies if the most distant object is at infinity.

1) Full Bercovitz formula

B = P(LN/(L-N)) (1/F - (L+N)/2LN)

B = Stereo Base (distance between the camera optical axes)
P = Parallax aimed for, in mm on the film
L = Largest distance from the camera lens
N = Nearest distance from the camera lens
F = Focal length of the lens

L-N = T = the front to back thickness of the subject.
With a bit of luck it is also the depth of field of the image, but does not have to be, especially at macro and telephoto distances where a big depth of field is hard to achieve.

The formula is not for orthoscopic viewing.
     orthoscopic viewing.

When you focus the camera it is best to focus between the nearest and furthest object and then stop down until both are in focus. This is using the hyperfocal distance, as marked on the lens barrel, to get an evenly sharp picture.
This sensible focusing manoeuvre is included in the formula, to allow for magnification of stereoscopic parallax resulting from the lens being racked forward from its infinity setting.

(Linear parallax = MAOFD: Maximum allowable on film deviation)

2) Simpler Bercovitz formula when Longest distance is infinity

B = P (N/F - 1/2)

This is sometimes quoted as B = PN/F, but the simple version only works if the lens is focussed on infinity. Most people focus closer than infinity, usually on the nearest object, using digital auto-focus. Experts focus onto the hyperfocal distance. Some Canon cameras do this hyperfocal computation directly, after you have focussed on the closest object and then on the most distant. The camera then adjusts the f number and the focus, so everything is in focus at once. The version of the formula which includes 1/2 allows for focussing on the hyperfocal distance.

.

Corrections to Bercovitz formula to avoid excessive stereoscopic depth in close-ups.

1. Davis modification: an arbitrary adjustment
2. Wattie modification: for correct stereoscopic perceived depth (roundness)

1) Davis Modification

The Bercovitz formula requires such a large stereo base for very shallow close-up objects that the resulting stereo depth magnification can distort and become disturbing.
This is avoided in practice by only using the uncorrected Bercovitz formula when the most distant plane (L) is more than twice as far away as the near plane (N).

Once L is less than 2N, the Bercovitz formula is adjusted by making

L = 2N

This stops the stereo base getting absurdly big. LINK

The Davis correction is built-in to the
Di Marzio formulae.

Di Marzio equation

Frank Di Marzio presents the Bercovitz equation as:

B = P (LN/(L-N)) (1/F - 1/S)

S = The distance focused on for maximum depth of field
S = 2LN/(L+N)

Di Marzio proceeds to simplify until:

B = H/60

H = the hyperfocal distance that has the near and far points in focus.

(I (Wattie) pointed out that H varies with the diameter of the circle of confusion which is chosen, making the formula not quite so universal as Frank hoped. Worse than that, hyperfocal distance and depth of field depends on the size of the image recording CCD, as discussed later. Also, modern digital cameras usually do not have the hyperfocal distances marked on the lenses - which are usually zoom lenses and usually do not give the focal length either. I am sorry Frank died before all this could be discussed with him and I only had time to demonstrate to him that depth of field was based on image magnification in the camera (reproduction ratio).

Meindre formula

Pierre Meindre provides a calculator suitable for a PDA or computer running html based on a simplification of the Bercovitz formula. This simplification excludes the S factor of Di Marzio and can be called a "pin-hole formula," since it does not involve focusing the camera. He warns of this by saying it will only work when the closest distance is quite a lot more than the focal length, which excludes close-ups. (Actually in practice the Meindre formula works "near enough" down into the low magnification close-up range, but certainly not in the macro range.)

You should use Meindre's formula for standard stereoscopic photography, since you can work it out on a pocket calculator.

Base = (P/F) * (LN/(L-N))

Stereo Base when the longest distance is infinity

By re-arranging the Bercovitz infinity formula, it is possible to compute how close the nearest object (N) "should be" when changing the stereo base and using a telephoto lens.  
stereo base

N = ( BF/P ) + F/2

The graph shown here was prepared by the author for 

Telephoto hyperstereoscopy with reduced subject depth

As in close-up stereoscopy, the stereo base can be increased if you do NOT include photographic infinity. The size of this correction can be very significant. It is well worth knowing in forest photography, where infinity is obscured by the trees.  This means stereoscopic infinity can be replaced by the deepest plane in the picture.

For example, using the full Bercovitz formula:

• 300mm lens
• N = 100 meters
• L = 150 meters

B (stereo base) = 120cm

If infinity is included in the picture, then B falls to 40cm

Photographic "infinity" is not mathematical infinity. It is a rather silly term for distance from the camera beyond which everything is in focus when the lens is set at its focal length from the film. Beyond photographic "infinity," things still get smaller as the distance is increased further still.

.

---

Image size set by the stereo base

"Frozen magnification."

An equation derived by John Wattie, where the camera is focussed on the hyperfocal distance and not on infinity shows:

Focal length drops out of the Bercovitz infinity formula and
Magnification in stereoscopic photography depends on the
Base and the linear
Parallax.

M = 1/(B/P - 1/2)

The consequences of this are discussed here

An even simpler version is provided by Dr T (George Themelis) using a "pin-hole" derivation where the lens does not have to be focussed, but it works pretty well in ordinary photography:

M = P/B

.

Choice of Linear Parallax (MAOFD)
(Maximum Acceptable On Film deviation)

The Bercovitz formula allows any linear parallax (MAOFD) to be set with precision.

Just what Parallax to choose depends on how the stereo pair will be viewed and the stereoscopic experience of the audience. 3D photographers often under-estimate the difficulty beginners have to diverge their eyes and adjust focus simultaneously. The MAOFD suitable for neophytes is far smaller than the experienced photographer can handle himself.

• The stereo pair is processed so the closest object is on, or rarely in front of the computer window (zero parallax).
• This is opposite to how you take a stereo picture, where the most distant objects stay still in each camera view finder, while the nearest objects move closer to each other.
• The MAOFD chosen will determine the separation between homologous objects at infinity on the final stereo pair.
  (Homologous object: the same object as seen in each of the stereo pictures.)
• In normal life objects at infinity are seen with the eye's optical axes parallel.
• Beginners to stereoscopic viewing have difficulty relaxing their eyes to parallel.
• The stereo image is actually flat on the screen or print, so looking to infinity requires the eyes to stay focused on the screen, while simultaneously diverging. The brain wants its eyes to refocus to infinity if they are diverged to parallel and for 3D viewing this has to be over-ruled. Challenging the brain is a way to cause headaches and nausea but experienced people soon adapt and have no problems.
• The eye divergence required is set by the infinity separation in the stereo pair. This separation is most easily measured on an anaglyph, where homologous points at the longest distance have different colours.
• The infinity separation expressed as a fraction:
  deviation / image width
  is the same no matter how much the image is magnified, making it a good measure of deviation and is classically 1/30. (Obviously this is not true if the picture is a panorama, or cropped to portrait format, but only applies to standard format images.
  For computer work it was better to think of
  deviation/computer monitor width)
  but modern monitors are all 16:9, letterbox format and that recommendation no longer applies!
  It might be sensible to change to deviation/monitor height, but that is an idea of the author's which does not have approval of the rest of the stereo community.
  
• It is often easier to see projected stereo than computer stereo. The eyes focus on the projection screen, which is further away than a computer monitor. There is less discrepancy between eye divergence and focus.
• Any difficulty seeing in 3D is usually resolved by moving further away from the computer or projection screen.

This is hyperstereoscopy, which some people have difficulty fusing when seen at full size. The deviation is 1/10 rather than the recommended 1/30.
However infinity separation on a 336mm monitor (horizontal width of a 17 inch monitor) is only 33mm, which is much less than your interocular distance. People experienced with 3D viewing should have no difficulty.

Click the image of Lake Wanaka to see it bigger on Flickr, then choose all images sizes.
This is a popular image on Flickr, which implies that most people have no trouble with the deviation.

Impression of depth

There is controversy about the impression of depth. Some say the depth impression should be realistic. Others say viewing must be comfortable, but that unreal depth is perfectly acceptable, even encouraged, as in hyperstereoscopy of the sun. Parallax and perceived stereo depth should be in harmony: the sun should look round like a ball and not flat or conical.

The maker of stereo pairs for computer viewing cannot control the screen size or where the audience will sit and so "impression of depth" becomes a hazy concept. When stereo is projected to an audience, only one person at a time can sit in the best possible seat in the house for seeing ortho stereo.

The formulae compute a base to give consistent stereo parallax.

• You have a choice to make this parallax large for experts, or small for neophytes.
• Maximum possible parallax is not always needed, as computed in spreadsheet 1. The art of 3D photography comes in here, it is not all science and mathematics.
• To be both consistent and conservative, (which some people who hate the constant deviation rule say they are) ignore the longest distance (which usually is very difficult to measure anyway) and always assume it is infinity.  This means only using the much simpler spread-sheet 2. (At the expense of some flat 3D at times).
• While anaglyphs can be shown with bigger parallax than stereo pairs, there is a school for minimal parallax, as this gives less ghosting and allows the "flat" image, when seen without goggles, to look almost normal. Commercial 3D workers use this method (e.g. Mirachrome anaglyphs by Alan Silliphant and "no shift" anaglyphs from Guglielmo Menagatti.)

1/30 rule

The 1/30 "rule" comes from the first treatise on stereo photography by Brewster who expressed it as an angular parallax of 2 degrees. The two degree rule only works for standard focal length lenses, which makes it useless for modern zoom lenses.

Nowadays the 1/30 rule is best expressed in terms of the final stereo image as:
"linear parallax at infinity measuring 1/30 of the width of a landscape format, 4:3, picture."

4:3 is the format of your computer screen (unless you are using a "letter-box" shape). This definition avoids big problems which arise with telephoto lenses, which were impossible on antique stereoscopic cameras, and fits in with the ISU definition.

(60mm infinity separation on your computer screen is equivalent to a "1/5 rule," which represents the theoretical limit for anaglyphs, but would be hopeless for a parallel stereo pair.)

Ramped stereo

Beginners more easily handle stereo parallax when it increases continuously into the distance ("ramped stereo").

Neophytes do not like close objects separated by a gap from distant objects ("stepped stereo"). They notice double vision, which is less obvious if their eyes glide smoothly into the depth. This may also explain why people often prefer a 3D picture taken from under an over-hang (tree branches meeting above a path for example.) This give another "stereo ramp" into the distance.

It is wise to start a stereoscopic projection show with gentle stereo (small, ramped parallax) and introduce bigger parallax as the show progresses, so the audience has time to adapt.

Projection stereo

In the ideal situation the audience should sit close to the screen so that it covers 40 degrees of their field of view. This is about the same as a person sitting at a computer and about the same as recorded by a 50mm  lens on 35mm film. Only one person can sit dead centre and see 40 degrees and he is said to be in the "ortho-stereo seat"

In practice in a hall, people all want to sit well back, far behind the ortho-stereo seat. This has the fortunate side effect that the stereo angular parallax is reduced. Even stereo incompetents can fuse the 3D. In this situation people even enjoy deep stereo, which at a computer monitor only stereo experts can fuse.

Danish anaglyph experiments on computer monitors: what should P be set to?

Experiments by Louis Carlsson on anaglyphs shows Danish "Vikings" (his term), who are not trained in stereoscopic vision, can handle a far point separation of 18mm on a computer screen at the usual viewing distance.
The near point separation (in front of the screen surface) that the general public can handle is 5mm.
According to Carlsson, anaglyph stereoscopic space for untrained people should be set in the range of :
-5mm to +18mm. Total separation 23mm.

18mm on a 17 inch (336mm horizontal) computer monitor is equivalent to a 35mm camera parallax setting (MAOFD) when taking the stereo pair of 1.8mm. So enter a maximum of 1.8mm into the above spreadsheets when using 35mm format for anaglyphs. (Effectively a 1/20, rather than the hallowed 1/30 rule.)

For digital cameras, enter 35mm equivalent focal lengths but not the tiny true focal length and still set Parallax to 1.8mm.
If objects are desired to project in front of the window ("poke your eyes out stereo" or "pop-out"), increase the total parallax setting to 2.4mm.

StereoPhotoMaker program (SPM) automatically adjusts maximum deviation, during post-processing, to 1/25, which is equivalent to P = 1.4mm. You can over-ride this if you wish by adjusting the separation of the two images (using the horizontal arrow keys). Often you do have to over-ride SPM automatic setting if the stereo base during photography has been "too big", in order to get the stereo window just where you want it. You do this at the expense of getting a wide infinity deviation, which neophytes may not be able to tolerate.

Anaglyphs set up for minimum ghosts, or red enhancement in the Mirachrome system, should have a 35mm equivalent parallax setting of 0.6mm or even less.

People having difficulty fusing computer 3D should just move further away from the computer screen.

1.8mm MAOFD is for anaglyphs and does NOT apply to stereoscopic slides or Holmes cards, where the 3D infinity separation is set by the viewing system and picture mounting technique required for two separate images. For slides and Holmes cards you must stick with MAOFD of 1.2mm maximum.

Exhaustive review of parallax / deviation / MAOFD etc, all meaning much the same thing.

.

---

Bercovitz formula spread-sheets

DOWNLOAD: Spreadsheet 1.2
(Compute stereo base: full Bercovitz formula: from macro to hyper stereo: Davis correction included: measure N from maps or pacing: camera screen magnification method also included.)

DOWNLOAD: Spreadsheet 2.2
(Simple version: Compute Nearest allowable distance: Bercovitz formula when L is at stereoscopic infinity. Will also work fairly well when L is less than infinity, but gets rather hopeless as the magnification increases and is totally useless for close-up stereoscopy.)

DOWNLOAD: Spreadsheet 2.3
(Complex: Stereo base and Magnification: Compute image size on digital camera view screen. Bercovitz formula with Wattie modification allows stereo base to be assessed directly from the digital camera view screen. Explanation here)

Spreadsheet 1:
Longest and shortest distance, any parallax, any focal length.

Below is an example of Spreadsheet v 1.0 (improved versions now available).
It is possible to calculate distances from a map or from simple pacing, and computation for those is provided. A laser range-finder, as used for shooting or golf is ideal (but costs a heap - only for obsessive neurotics!)
The Excel spreadsheet works in a PDA running Windows (such as an iPaq), allowing use in the field.
It works very well with paired Sony V3 digital cameras, but will work with any camera.

If you do not know the 35mm equivalent focal length of your zoomed lenses, that is a problem and your rig is not really suitable for variable zoom, variable base, precision, stereo photography using this spreadsheet. Do not despair, it can still be done using Wattie's method of digital screen magnification.

Spreadsheet 2:
Longest distance always assumed to be infinity.

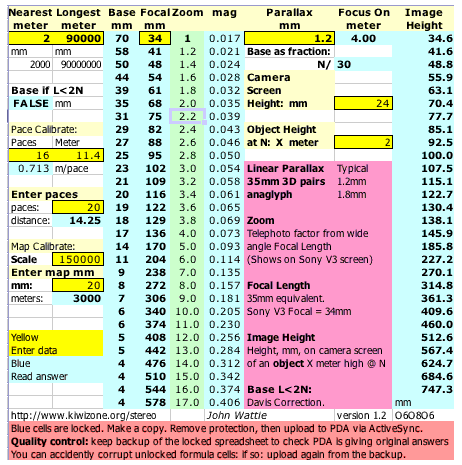
If you start with a fixed stereo base (in a Z mount for example) it helps to know the nearest distance you can go.

Ideal for landscapes, where infinity is in the picture. Modern cameras have zoom lenses and the table shows how the closest permitted distance varies as the lens is zoomed, stereo base changed and parallax varied.

People who used a stereo camera, with its unchangeable focal length and stereo base, will know they were not to go closer than 2 meters. This table is the equivalent rule for digital zoom cameras

Spread Sheet 2 Download.

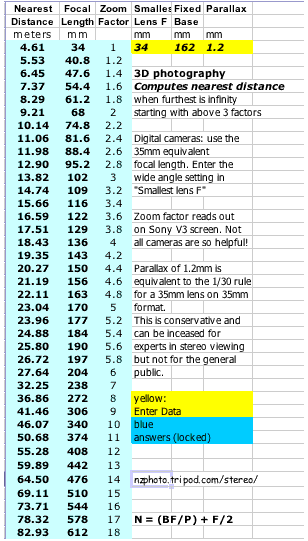
Fortunately Sony V3 cameras (frequently used for digital stereo since they can be synchronised accurately) quote the focal length as a multiplying factor on the screen. Wide angle on a Sony V3 is equivalent to 34mm. Telephoto zoom times 4 is equivalent to 136mm. ("Equivalent" means giving the same angle of view as a 35mm camera would do).

1.2mm parallax on the Sony V3 screen, which is 50mm wide, becomes
1.2 x 50/36 = 1.7mm
Still use 1.2mm in the formula.
Use 1.7mm if you are adjusting stereo base by directly measuring parallax on the camera screen. The formula operates with 35mm equivalent, not with actual size.

Remember that cropping the image during post processing and then enlarging it again is the same as using digital telephoto. So if you will crop the vertical height of the image to half and then bring up to full size in soft-ware, double the focal length setting in the above formulae.

Cropping horizontally is NOT a problem since it does not change the magnification of the final image.

Cropping vertically and then magnifying the picture to fill the screen is a problem. Magnification of the image is the same as using a telephoto lens. There is a fundamental difference between vertical cropping and resizing versus horizontal cropping for window corrections. The horizontal cropped picture cannot be magnified - if you try the vertical dimension will be too big for the screen.

See here for confusion about cropping.

Reduced depth impression with telephoto stereo:

Notice how the stereo base is inversely proportional to the focal length: double the focal length and the required stereo base halves.

Or, double the focal length and keep the base constant: the nearest allowable distance doubles.

The mathematics of telephoto depth is analysed in the PePax section

How to overcome reduced telephoto depth impression

To overcome the flattening of depth when using a telephoto lens, you must increase the stereo base by T/S, where:
T is the telephoto focal length and
S is the standard focal length.

Base increase = T/S

For example:

You want to take a head and shoulders stereoscopic portrait with a telephoto lens, rather than the standard lens.
(This is good photographic practice as professionals have used a longer focal length portrait lenses since one and a half centuries ago, so can it work in stereo?)

50mm Standard lens with a 65 mm stereo Base provides an orthostereoscopic view on 35mm format.
(Because 65mm is an adult interocular distance and you plan to view the stereo picture at a "normal" distance from the computer screen, or in a standard stereoscope with 50mm focal length lenses, to match the standard camera lens.)

Now use a 100mm Telephoto lens (twice standard), what Base is needed for an orthostereoscopic view?
(Edition 2: this is not orthostereoscopic but it is orthoplastic.)

Base increase = T/S = 100/50 = 2
Base for "orthostereoscopic depth" = 2 x 70mm = 140mm

Note that this is a constant magnification situation, since you want the portrait to be a standard head and shoulders view. (PePax requires a constant magnification).

There are three problems:

1. The depth impression is only correct for the portrait,
2. Objects further away are too big (wrong perspective) and show decreasing depth.
3. Infinity cannot be included in the picture, or stereoscopic disparity will be too big.

You will probably conclude this is a fair compromise, since:

1. you want to have a close background for the portrait anyway and
2. the reduced perspective is just fine for overcoming familiar photographic artefacts, like the nose seeming to project too far forwards on standard focal length portraits.

The Base increase = T/S formula works well for stereoscopic wild-life photography, where telephoto lenses are essential to avoid disturbing the animals. Just remember, it only works if the background is close behind the animal. You cannot make this work for a Stag on a Crag, with a distant mountain behind him. The Bercovitz formula would never permit that!

Bercovitz curves are available in graph form { here }

Practical Examples from using the formulae

.